In the Part 2 tutorial, I would like to continue the topic on stock price prediction and to endow the recurrent neural network that I have built in Part 1 with the capability of responding to multiple stocks. In order to distinguish the patterns associated with different price sequences, I use the stock symbol embedding vectors as part of the input.
Dataset
During the search, I found this library for querying Yahoo! Finance API. It would be very useful if Yahoo hasn’t shut down the historical data fetch API. You may find it useful for querying other information though. Here I pick the Google Finance link, among a couple of free data sources for downloading historical stock prices.
The data fetch code can be written as simple as:
| |
When fetching the content, remember to add try-catch wrapper in case the link fails or the provided stock symbol is not valid.
Model Construction
The model is expected to learn the price sequences of different stocks in time. Due to the different underlying patterns, I would like to tell the model which stock it is dealing with explicitly. Embedding is more favored than one-hot encoding, because:
- Given that the train set includes $N$ stocks, the one-hot encoding would introduce $N$ (or $N-1$) additional sparse feature dimensions. Once each stock symbol is mapped onto a much smaller embedding vector of length $k$, $k \ll N$, we end up with a much more compressed representation and smaller dataset to take care of.
- Since embedding vectors are variables to learn. Similar stocks could be associated with similar embeddings and help the prediction of each others, such as “GOOG” and “GOOGL” which you will see in Fig. 5. later.
In the recurrent neural network, at one time step $t$, the input vector contains input_size (labelled as $w$) daily price values of $i$-in stock, ($p_{i, t w}, p_{i, t w+1}, \ldots, p_{i,(t+1) w-1}$). The stock symbol is uniquely mapped to a vector of length embeddingsize (labelled as $k$), $\left(e{i, 0}, e*{i, 1}, \ldots, e*{i, k}\right)$. As illustrated in Fig. 1., the price vector is concatenated with the embedding vector and then fed into the LSTM cell.
Another alternative is to concatenate the embedding vectors with the last state of the LSTM cell and learn new weights $W$ and bias $b$ in the output layer. However, in this way, the LSTM cell cannot tell apart prices of one stock from another and its power would be largely restrained. Thus I decided to go with the former approach.
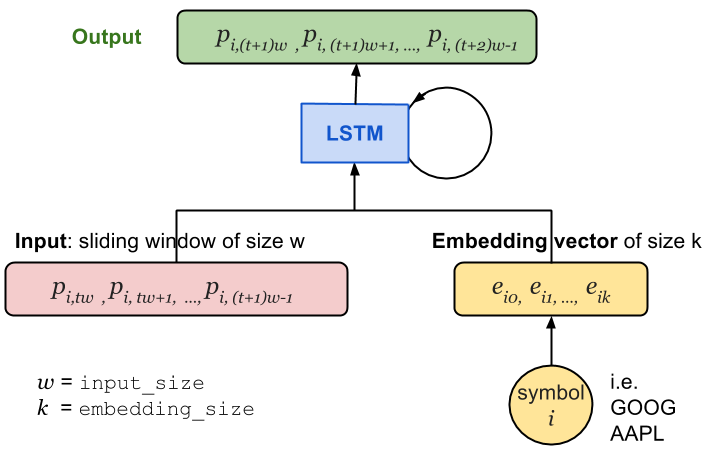
Fig. 1: The architecture of the stock price prediction RNN model with stock symbol embeddings.
Two new configuration settings are added into RNNConfig:
embedding_sizecontrols the size of each embedding vector;stock_countrefers to the number of unique stocks in the dataset.
Together they define the size of the embedding matrix, for which the model has to learn embedding_size $\times $ stock_count additional variables compared to the model in Part 1.
Define the Graph
— Let’s start going through some code —
(1) As demonstrated in tutorial Part 1: Define the Graph, let us define a tf.Graph() named lstm_graph and a set of tensors to hold input data, inputs, targets, and learning_rate in the same way. One more placeholder to define is a list of stock symbols associated with the input prices. Stock symbols have been mapped to unique integers beforehand with label encoding.
(2) Then we need to set up an embedding matrix to play as a lookup table, containing the embedding vectors of all the stocks. The matrix is initialized with random numbers in the interval [-1, 1] and gets updated during training.
| |
(3) Repeat the stock labels num_steps times to match the unfolded version of RNN and the shape of inputs tensor during training. The transformation operation tf.tile receives a base tensor and creates a new tensor by replicating its certain dimensions multiples times; precisely the $i$-th dimension of the input tensor gets multiplied by multiples[i] times. For example, if the stock_labels is [[0], [0], [2], [1]] tiling it by [1, 5] produces [[0 0 0 0 0], [0 0 0 0 0], [2 2 2 2 2], [1 1 1 1 1]].
| |
(4) Then we map the symbols to embedding vectors according to the lookup table embedding_matrix.
(5) Finally, combine the price values with the embedding vectors. The operation tf.concat concatenates a list of tensors along the dimension axis. In our case, we want to keep the batch size and the number of steps unchanged, but only extend the input vector of length input_size to include embedding features.
The rest of code runs the dynamic RNN, extracts the last state of the LSTM cell, and handles weights and bias in the output layer. See Part 1: Define the Graph for the details.
Training Session
Please read Part 1: Start Training Session if you haven’t for how to run a training session in Tensorflow.
Before feeding the data into the graph, the stock symbols should be transformed to unique integers with label encoding.
The train/test split ratio remains same, 90% for training and 10% for testing, for every individual stock.
Visualize the Graph
After the graph is defined in code, let us check the visualization in Tensorboard to make sure that components are constructed correctly. Essentially it looks very much like our architecture illustration in Fig. 1.
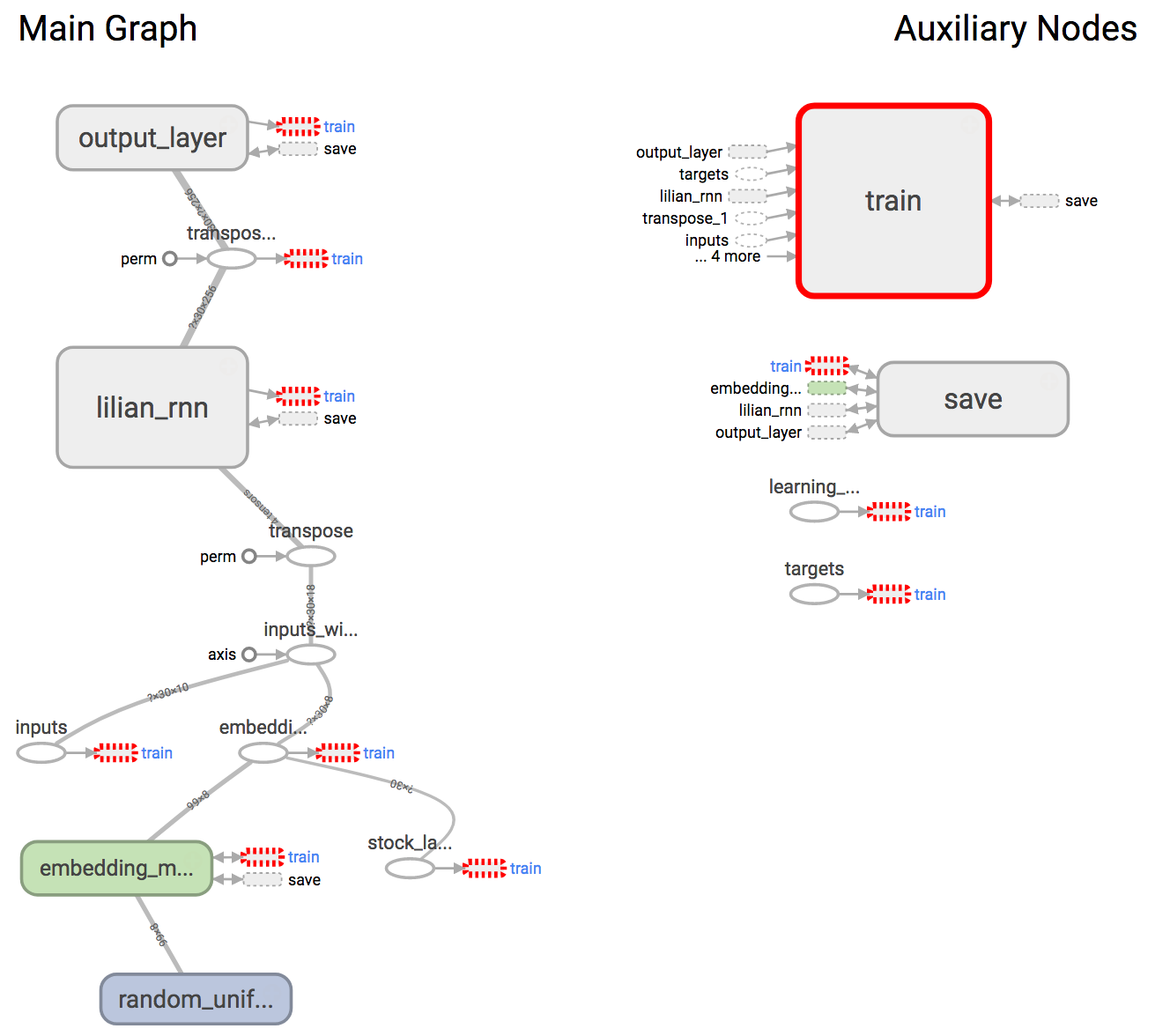
Fig. 2: TensorBoard visualization of the graph defined above. Two modules, “train” and “save,” have been removed from the main graph.
Other than presenting the graph structure or tracking the variables in time, Tensorboard also supports embeddings visualization. In order to communicate the embedding values to Tensorboard, we need to add proper tracking in the training logs.
(0) In my embedding visualization, I want to color each stock with its industry sector. This metadata should stored in a csv file. The file has two columns, the stock symbol and the industry sector. It does not matter whether the csv file has header, but the order of the listed stocks must be consistent with label_encoder.classes_.
(1) Set up the summary writer first within the training tf.Session.
(2) Add the tensor embedding_matrix defined in our graph lstm_graph into the projector config variable and attach the metadata csv file.
| |
(3) This line creates a file projector_config.pbtxt in the folder your_log_file_folder. TensorBoard will read this file during startup.
| |
Results
The model is trained with top 50 stocks with largest market values in the S&P 500 index.
| |
And the following configuration is used:
Price Prediction
As a brief overview of the prediction quality, Fig. 3 plots the predictions for test data of “KO”, “AAPL”, “GOOG” and “NFLX”. The overall trends matched up between the true values and the predictions. Considering how the prediction task is designed, the model relies on all the historical data points to predict only next 5 (input_size) days. With a small input_size, the model does not need to worry about the long-term growth curve. Once we increase input_size, the prediction would be much harder.
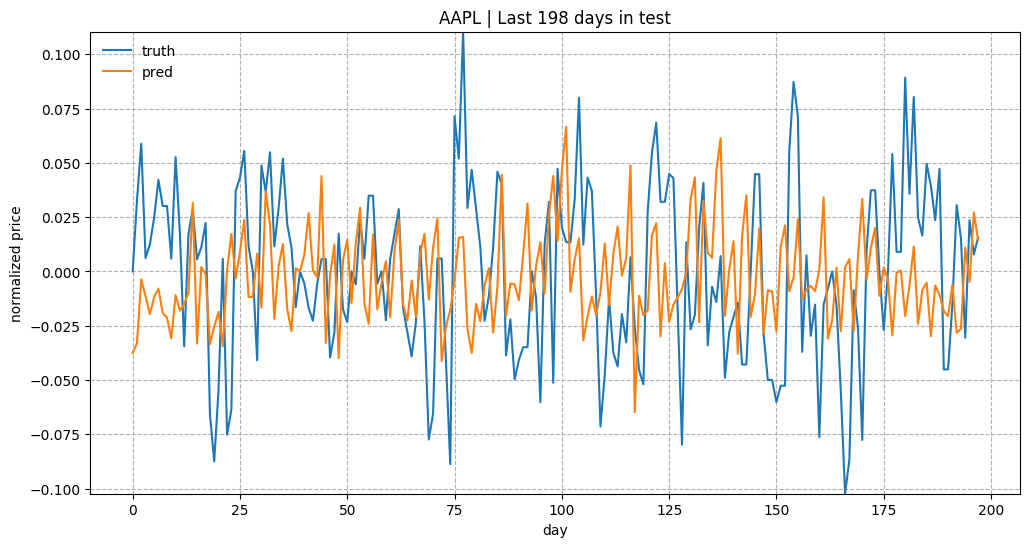
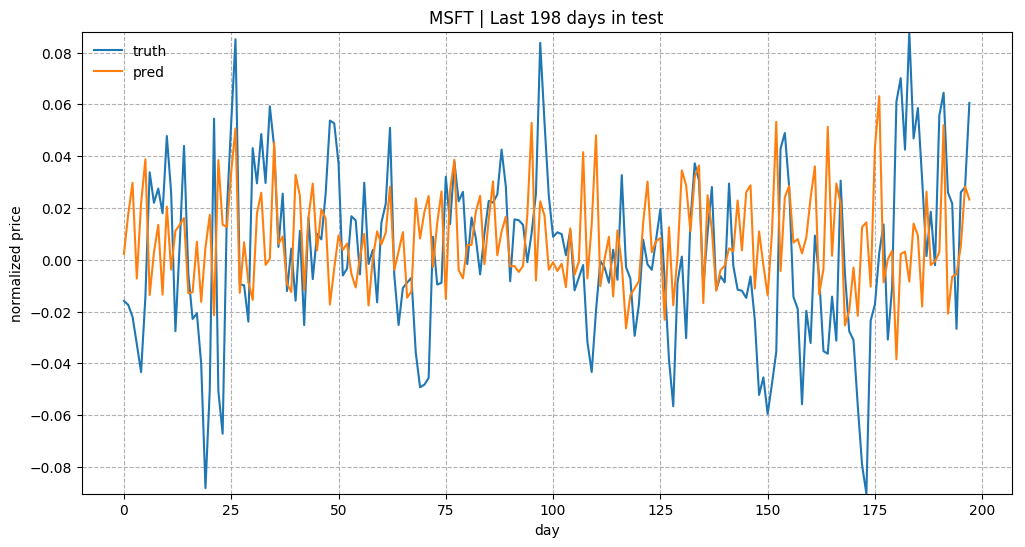
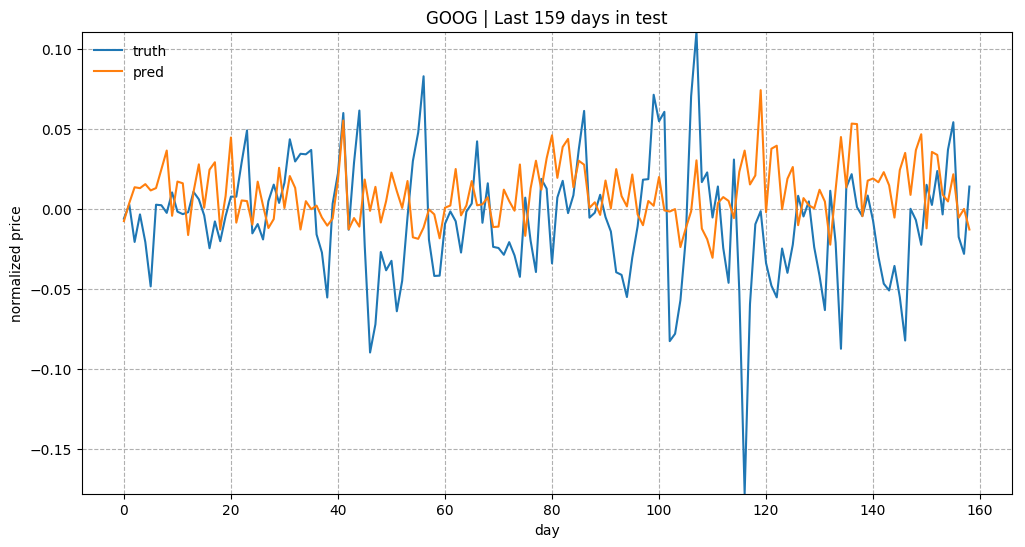
Fig. 3: True and predicted stock prices of AAPL, MSFT, and GOOG in the test set. The prices are normalized across consecutive prediction sliding windows (See Part 1: Normalization.) The y-axis values get multiplied by 5 for a better comparison between true and predicted trends.
Embedding Visualization
One common technique to visualize the clusters in embedding space is t-SNE (Maaten and Hinton, 2008), which is well supported in Tensorboard. t-SNE, short for “t-Distributed Stochastic Neighbor Embedding, is a variation of Stochastic Neighbor Embedding (Hinton and Roweis, 2002), but with a modified cost function that is easier to optimize.
- Similar to SNE, t-SNE first converts the high-dimensional Euclidean distances between data points into conditional probabilities that represent similarities.
- t-SNE defines a similar probability distribution over the data points in the low-dimensional space, and it minimizes the Kullback–Leibler divergence between the two distributions with respect to the locations of the points on the map.
Check this post for how to adjust the parameters, Perplexity and learning rate (epsilon), in t-SNE visualization.
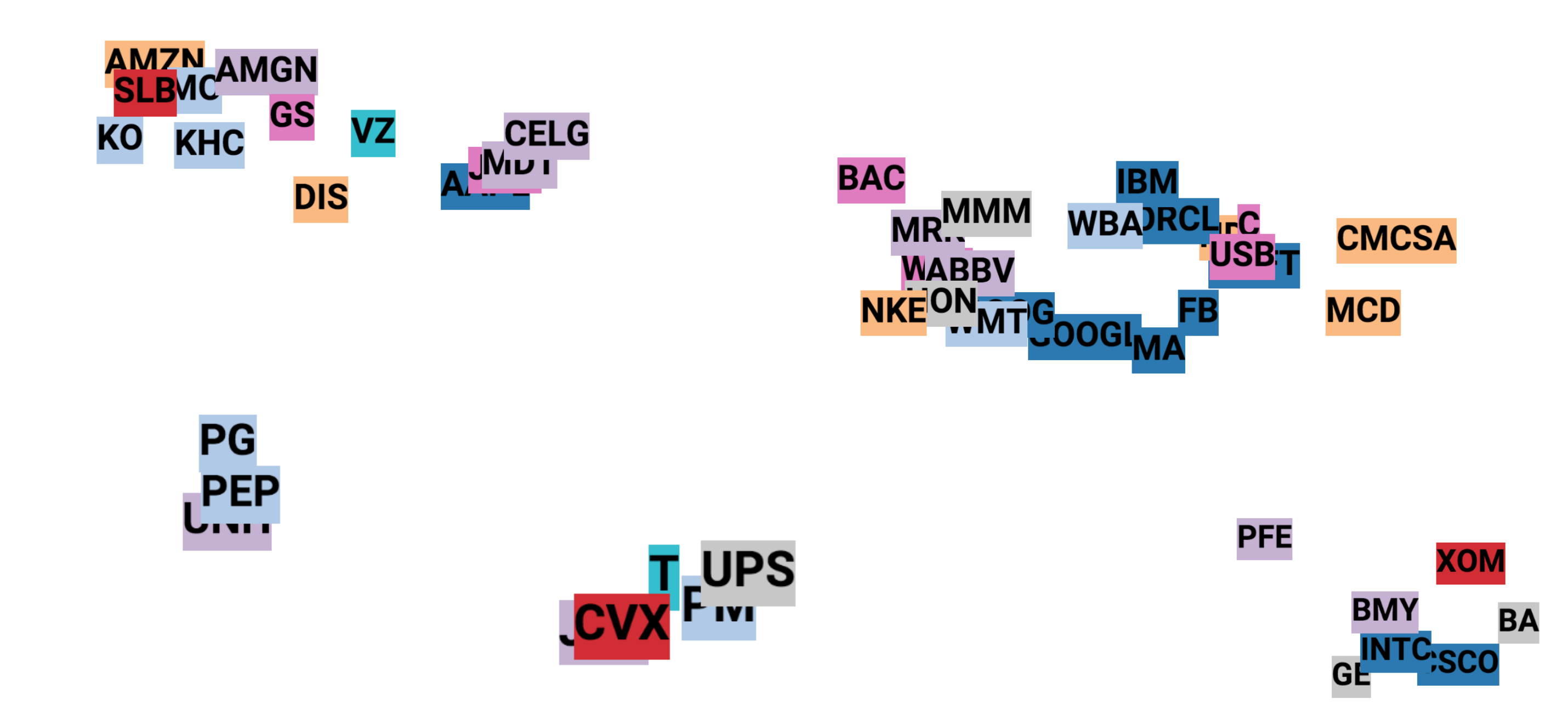
Fig. 4: Visualization of the stock embeddings using t-SNE. Each label is colored based on the stock industry sector. We have 5 clusters. Interestingly, GOOG, GOOGL, and FB belong to the same cluster, while AMZN and AAPL stay in another.
In the embedding space, we can measure the similarity between two stocks by examining the similarity between their embedding vectors. For example, GOOG is mostly similar to GOOGL in the learned embeddings (See Fig. 5).
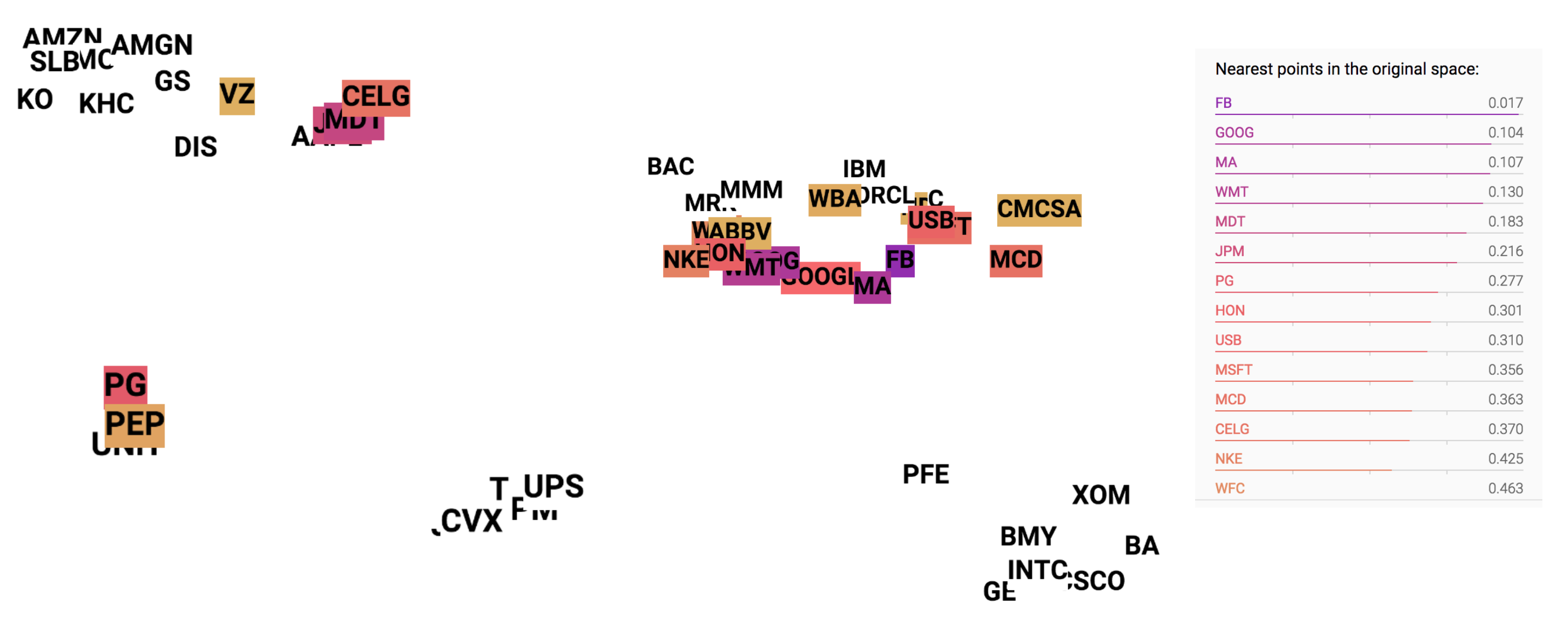
Fig. 5: “GOOG” is clicked in the embedding visualization graph, and the top 20 similar neighbors are highlighted with colors from dark to light as the similarity decreases.
Known Problems
- The prediction values get diminished and flatten quite a lot as the training goes. That’s why I multiplied the absolute values by a constant to make the trend is more visible in Fig. 3., as I’m more curious about whether the prediction on the up-or-down direction right. However, there must be a reason for the diminishing prediction value problem. Potentially rather than using simple MSE as the loss, we can adopt another form of loss function to penalize more when the direction is predicted wrong.
- The loss function decreases fast at the beginning, but it suffers from occasional value explosion (a sudden peak happens and then goes back immediately). I suspect it is related to the form of loss function too. A updated and smarter loss function might be able to resolve the issue.